TEORÍA DE CONJUNTOS
CONJUNTOS: Un conjunto es una agrupación de objetos, llamados elementos, con un criterio que permiten identificar cuando un objeto determinado pertenece o no a la agrupación.
Los conjuntos se designan con letras mayúsculas, A, B, C, D… X, Y, Z. En cambio los elementos que forman el conjunto se simbolizan con letras minúsculas: a, b, c… x, y, z.
DETERMINACIÓN DE CONJUNTOS
Cuando se expresa un conjunto es importante determinarlo de tal forma que se pueda decir si un elemento le pertenece o no.
Por extensión, nombrando uno a uno todos los elementos del conjunto. Por ejemplo.
B: (2, 3, 5, 7, 11,13, 17, 19.)
Por comprensión, nombrando la propiedad común a todos los elementos. Por ejemplo, como B es un conjunto formado por todos los números primos menores que 20 se escribe.
B:(X/X es un numero primo menos que 20)
RELACIÓN ENTRE CONJUNTOS
RELACION ENTRE CONJUNTOS
INCLUSIÓN: Cuando todos los elementos de A están incluidos en B. Se representa como A [ B
IGUALDAD: Cuando dos conjuntos A y B son iguales y se simboliza A=B
INTERSECANTES: Cuando dos conjuntos A y B tienen elementos comunes pero.
DISYUNTAS: Dos conjuntos A y B son disyuntos cuando no tienen ningún elemento en común.
OPERACIÓN ENTRE CONJUNTOS
UNIÓN ENTRE CONJUNTOS: La unión entre dos conjuntos A y B es el conjunto formado por elementos que pertenecen tanto A como a B. La unión de dos conjuntos A y B se nota AUB.
INTERSECCIÓN ENTRE CONJUNTOS: La intersección de dos conjuntos formados por los elementos que pertenecen al conjunto A y al conjunto B. Se simboliza A ∩ B.
COMPLEMENTO DE UN CONJUNTO: El complemento de un conjunto A contenido en un conjunto universal U pero que no están el conjunto A. el complemento se escribe AC.
DIFERENCIA ENTRE CONJUNTOS: La diferencia de dos conjuntos A y B es el conjunto formado por todos los elementos que pertenecen al conjunto A y que no pertenecen al conjunto B. La diferencia se simboliza A-B.
TRABAJO EVALUATIVO SOBRE CONJUNTOS
La presente evaluación se realiza con el fin de analizar el trabajo realizado durante la clase sobre conjuntos, esta evaluación es un punto más del trabajo ya que se presenta esta actividad con el fin de evaluar por medio de competencias en el área de matemáticas.
1. Determine cada conjunto por extensión.
· F= (partes de la flor)
F= (______________________________________)
· A= (meses de 31 dias)
A= (______________________________________)
2. Nombre dos conjuntos por comprensión.
· D=(_________________________)
· R= (__________________________)
3 . E Escribe el signo ϵ y ϵ o la letra del conjunto según corresponda
· P = (NUMEROS PRIMOS) * T = (6,9,10,14,15,18) * M= (MULTIPLOS DE 4)
- 4 _____ P - 10 ______ M - 11 ______ T
- 14 _______ T - 2 _______ P - 13 ______ P
- 18 ______ M - 6 _______ T - 8 _______ P
4. Escribe en un diagrama, los nombres de los niños que se inscriben en un intercolegiado, algunos de ellos participa más de un deporte.
x
F B
Felipe Jaime
Andres David
Sergio Pablo
David Andres
VÍDEO TEORÍA DE CONJUNTOS GRADO SEXTO
CONJUNTOS (DEMUESTRA LO APRENDIDO)
Observa atentamente el siguiente vídeo, luego deja un comentario en el Blog donde respondas las preguntas al siguiente caso: Sea el conjunto del reino animal
1. Menciona 5 elementos de éste conjunto.
2. ¿Qué se puede decir del elemento "Teléfono" respecto del conjunto planteado?
3. ¿Cuál sería el conjunto universal en éste caso?
4. ¿Éste conjunto es finito o infinito?
PARA MAS INFORMACIÓN HACER CLIC AQUÍ
PROF. JOSE PEÑA M
NUMERACIÓN
¿Porqué surgió la necesidad de numerar?
Cuando trabajamos con objetos a veces tenemos la necesidad de numerarlos, es decir de ordenarlos. Desde tiempos muy remotos el hombre sintió la necesidad de contar sus rebaños, de hacer trueques, de realizar intercambios comerciales, de llevar un calendario que les permitiera saber cuál era la mejor época para la siembra y cuándo debían recogerla. Por ello había que contar los días y utilizaban números naturales.
Se ha tenido la necesidad de contar mucho antes que la de escribir, pero la utilización de la numeración actual, incluyendo el cero, es muy reciente.
La representación numérica de la nada, o sea, el surgimiento del cero, es uno de los avances más importantes de la civilización humana y se produjo hace más de 1300 años, siendo los hindúes sus responsables. Con él, se podría representar cualquier cantidad grande o pequeña sin riesgo de error.
No se sabe a ciencia cierta cual fue la fecha exacta en la que se comenzó a contar pero lo que sí es evidente que debieron ayudarse de ciertas herramientas e incluso empezaron a utilizar las múltiples fuentes de referencia de la naturaleza.
¿Qué es un sistema de numeración?
Debida a la necesidad de numerar, cada cultura estableció un sistema adecuado de numeración y de símbolos para poder llevar a cabo todo lo dicho anteriormente.
Sistema de numeración actual
El sistema de numeración actual es el sistema decimal o sistema en base diez. Se llama así porque se utilizan diez dígitos para representar todos los números.
En esta imágen podemos observar el proceso.
Paso de decimal ( con decimales) a binario:
Continuamos por la parte decimal., ahora cada decimal se multiplica por 2. Si el resultado de la multiplicación es mayor o igual a 1, se escribe como 1, si el resultado es menor que 1, se escribe 0 porque en binario solo se toma la parte entera del resultado.
Como ya sabemos, un sistema de numeración es un conjunto de símbolos y reglas de generación que permiten construir todos los números válidos.
Actualmente, aplicamos varios sistemas de numeración en nuestro día a día para resolver problemas que se nos puedan presentar. Hablamos de:
• Sistemas de numeración no posicionales: son los más primitivos. Por ejemplo en uso de los dedos de la mano o incluso las manos y el uso de cuerdas con nudos para representar la cantidad.
•Sistemas de numeración posicionales: es un modo de escritura numérica en el cual, cada dígito posee un valor diferente que depende de su posición relativa. Queda determinada por la base, que es el número de dígitos necesarios para escribir cualquier número.
El sistema de numeración actual es el sistema decimal o sistema en base diez. Se llama así porque se utilizan diez dígitos para representar todos los números.
Según la antropología el sistema decimal está en los diez dedos que tenemos en las manos, los cuales siempre nos han servido para contar. El sistema decimal es un sistema de numeración posicional, por lo que el valor del dígito puede variar según su posición dentro del número.
Los dígitos adoptan un valor u otro según su posición, por lo que diez unidades forman una decena, diez decenas forman una centena, diez centenas forman una unidad de mil, diez unidades de mil forman una decena de mil, diez decenas de mil forman una centena de mil, diez centenas de mil forman una unidad de millón, diez unidades de millón forman una decena de millón y diez decenas de millón forman una centena de millón.
¿Qué es el sistema binario?
En el campo científico y matemático es un sistema de numeración donde los números se representan utilizando sólo el 0 y 1.
El sistema binario se usa, principalmente, en el campo informático. Todos los ordenadores usan este sistema de numeración.
Paso de decimal a binario:
Para pasar de decimal a binario, se comienza dividendo el número entre 2. No importa si hay resto o no, hay que seguir dividendo hasta que el número a dividir sea 1.
Una vez hecha la división se cogen los restos y se ordenan, desde el final hasta el principio. Ese es el número que buscamos en binario.
Una vez hecha la división se cogen los restos y se ordenan, desde el final hasta el principio. Ese es el número que buscamos en binario.
Paso de decimal ( con decimales) a binario:
Para pasar de decimal( con decimales a binario) se empieza con la parte entera: si es0, se escribe 0; si es 1, se escribe 1..
Continuamos por la parte decimal., ahora cada decimal se multiplica por 2. Si el resultado de la multiplicación es mayor o igual a 1, se escribe como 1, si el resultado es menor que 1, se escribe 0 porque en binario solo se toma la parte entera del resultado.
Finalmente, se colocan los números obtenidos en el orden de su obtención.
Paso de binario a decimal:
Para pasar de binario a decimal se empieza por la parte izquierda.
Cada cifra se multiplica por 2 elevado a la potencia del lugar que ocupa.
Después de multiplicar cada cifra, se suma y el resultado obtenido es el número en decimal. Cada cifra se multiplica por 2 elevado a la potencia del lugar que ocupa.
SISTEMA EN BASE 10
Esto quiere decir que el principio de agrupamiento de este sistema es diez, en donde cada 10 unidades se forma otra de carácter superior, la cual se escribe a la izquierda de la primera de las unidades. Esto es ilustrado en el ábaco, en donde cada vez que tenemos 10 fichas en una varilla, las transformamos en una de la varilla inmediatamente izquierda y la ubicamos en ésta, con lo cual obtenemos que 10 unidades equivales a una decena, que 10 decenas equivalen a 1 centena y así sucesivamente.
POSEE 10 DÍGITOS
Éstos son el: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 y su combinación puede formar infinitos números.
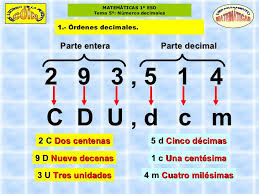
VALOR POSICIONAL Y RELATIVO DE CADA DÍGITO
Esto quiere decir que dependiendo de la posición en donde se ubique cada dígito el valor que éste tendrá.
Así por ejemplo, vemos que el valor del número 2 en 3.245 no es el mismo que en el 332, esto debido a que los dígitos actúan como multiplicadores de las potencias de la base.
Así tenemos que en el número 3.245 el 2 se ubica en las centenas, por lo que su valor posicional será de 2*100, es decir 200. Sin embargo, en el número 332 su valor equivaldrá a la multiplicación de 2*1, es decir 2, ya que el 2 se encuentra en la posición de las unidades. Por otro lado, si recordamos cuál es el valor de cada base tendremos:
| Unidades | 1 |
| Decenas | 10 |
| Centenas | 100 |
| Unidades de Mil | 1.000 |
| Decenas de Mil | 10.000 |
| Centenas de Mil | 100.000 |
Ejercicios sobre sistema decimal












.gif)
.gif)
.gif)

esta facil
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarTrabajo 1:
ResponderEliminar- Perro,gato,caballo,conejo y león.
- No pertenece.
- Reino animal
- Infinito
Bllena Pato Delfin Conejo Gato
ResponderEliminarNo pertenece
Reino animal
Infinito
saludos desde Peru
ResponderEliminarEste comentario ha sido eliminado por el autor.
EliminarKEVIN LIAN LUO 6° A
ResponderEliminar1° DELFIN,LEON,TIGRE,CONEJO,COBRA
2° NO PERTENECE
3° EL REINO ANIMAL
4° INFINITO
tamos con cr7 y messi 10
ResponderEliminarTrabajo 1:
ResponderEliminar1.Gato,leon,ballena,tigre y tiburón.
2.No pertenece al conjunto reino animal
3.El reino animal.
4.Es infinito.
Este comentario ha sido eliminado por el autor.
ResponderEliminar1.gato, perro, conejo, raton, caballo
ResponderEliminar2.No pertenece
3.Reino animal
4.Infinito
1.Leon,perro,gato,jirafa,delfin.
ResponderEliminar2.No pertenece.
3.El reino animal
4.Es infinito
1°-Perro,Gato,Elefante,Jirafa,Oveja
ResponderEliminar2°No pertenece
3°Los animales
4°Infinito
Este comentario ha sido eliminado por el autor.
ResponderEliminar?
Eliminar1.Gato,leon,ballena,tigre y tiburón
ResponderEliminar2.Que no pertenece
3.Los animales
4.Infinito
Frank Joseph Isique Caqui 6°C
ResponderEliminar1. Perro, león, tigre, puma y tiburón
2. No pertenece
3. El Reino Animal
4. Infinito
hola
ResponderEliminarHola :v
Eliminarhola :V
Eliminar1. Perro, león, gato, peces y elefante
ResponderEliminar2. No pertenece
3. Todos lo animales
4. Infinito
Saludas hacia todo Peru xd
Eliminarhola profe bien el vídeo
ResponderEliminarEste comentario ha sido eliminado por un administrador del blog.
ResponderEliminar- Perro,gato,caballo,conejo y león.
ResponderEliminar- No pertenece.
- Reino animal
- Infinito
es sierto
ResponderEliminarhola
ResponderEliminarlolololol
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarhola
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarHumpty???
ResponderEliminarEste comentario ha sido eliminado por el autor.
Eliminarhola mis amigus :D
ResponderEliminarno hablen
ResponderEliminara no es
ResponderEliminarEste comentario ha sido eliminado por un administrador del blog.
ResponderEliminarXDXDXDXDXD
ResponderEliminarholaaaaa
ResponderEliminarxdxdxdxd
ResponderEliminarta facil
ResponderEliminar