Teoría de conjuntos
Conjuntos
Debes aprender...
Un conjunto es la reunión de elementos que tienen una o mas características en común.
Para representar un conjunto, se agrupan sus elementos en una linea cerrada llamada diagrama, o se escriben sus elementos entre llaves.
Colocamos llaves en los elementos del conjunto.
F = { Pera, Fresa, Banano}
Clasificación de conjuntos
No se pueden enumerar P = {0, 1, 2, 3 …} todos sus elementos
Se pueden enumerar Q = {2, 4, 6, 8}
todos sus elementos.
Tiene un solo elemento. R = {7}
No tiene elementos. S = { }
Relación de contenencia
Sea G el conjunto de los animales que viven en la granja
Fíjate en los
subconjuntos
que podemos formar.
El conjunto A está contenido en el conjunto G = A Ì G
El conjunto N está contenido en el conjunto G = N Ì G
Intersección de conjuntos
¿Quiénes practican baloncesto y natación?
Hallamos los elementos comunes de B y N.
Ana y Beto
Practican baloncesto
El conjunto intersección está formado por los
elementos comunes de ambos conjuntos.
Intersección de conjuntos
Los conjuntos no tienen elementos comunes.
Unión de conjuntos
Para preparar su jugo de frutas, Gabriel separa los ingredientes en dos conjuntos.
Hallamos la unión de los conjuntos F y P.
El conjunto unión está formado por los elementos de ambos conjuntos.
¿Quiénes participarán en los concursos?
Hallamos la unión de los conjuntos M y D.
Ahora, observa la imagen
Martín dice que Manuela se equivocó al escribir que S Ì T.
Él afirma que hay elementos de S que no están en T.
¿Es correcta la afirmación de Martín?¿Por qué?
CLASIFICACIÓN DE CONJUNTOS
CLASES DE CONJUNTOS
Según el número de elementos que conforman un conjunto, éstos se clasifican en:
Universal o referencia.
§ Vacío.
§ Unitario.
§ Finito.
§ Infinito.
El conjunto universal o referencia, es el formado por un amplio número de elementos, como puede ser el conjunto de los números naturales o por letras del abecedario. Estos conjuntos sirven de base para crear más conjuntos.
Para representar que un conjunto es universal se utiliza la vocal Umayúscula.
Ejemplo:
El conjunto formado por las letras del abecedario.
U = { letras del abecedario }
Gráficamente:
Del conjunto U se puede formar el conjunto V de vocales y conjunto C de consonantes.
El conjunto vacío es aquel que no tiene elemento alguno.
Ejemplos:
A = { }
El conjunto A no posee ningún elemento.
B = { números impares entre 5 y 7 }
No existe ningún numero impar entre los números 5 y 7.
Gráficamente:
Generalmente el conjunto vacío se representa mediante un paréntesis { } (corchete sin elemento), o por el símbolo
Conjunto unitario
El conjunto unitario es aquel que posee solamente un elemento.
Conjunto finito
Un conjunto es finito, cuando posee un comienzo y un final, en otras palabras, es cuando los elementos del conjunto se pueden determinar o contar.
Ejemplos:
1. El conjunto de números naturales mayores de 8 y menores de 10:
C = { 9 }
El único elemento es el número 9.
. Conjunto de satélites naturales de la Tierra
S = { Luna }
El conjunto está formado por un solo elemento, porque la Tierra solo posee un satélite natural, la Luna.
Conjunto finito
Un conjunto es finito, cuando posee un comienzo y un final, en otras palabras, es cuando los elementos del conjunto se pueden determinar o contar.
Ejemplos:
- Conjunto de números pares entre 10 y 40:
R = { 10,12,14,16,18,20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40 }
- Conjunto de las páginas de un libro:
T = { páginas de un libro }.
- Conjunto de vocales.
V = { a, e, o, i, u }
Conjunto infinito 
El conjunto es infinito, cuando posee un inicio pero no tiene fin. Es decir, que la cantidad de elementos que conforman el conjunto no se puede determinar.
Ejemplos:
- El conjunto de los números naturales:
N = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,...}
El conjunto de los números naturales es infinito, puesto que no es posible contar la totalidad de elementos (números) que conforman el conjunto.
- El conjunto de los peces en el mar:
P = { los peces en el mar }
VEAMOS EL SIGUIENTE VIDEO DEL TEMA
PARA MAS INFORMACIÓN SOBRE EL TEMA HACER CLIK AQUI
RESUELVE EL CUESTIONARIO EN LA PLATAFORMA TANGUIS.NET

Problemas que se resuelven con conjuntos

Ante todo, compartimos nuevamente la letra del problema en cuestión:
- Problema 3
En una celebración de graduación, las 30 estudiantes del curso debatían acerca de la bebida que debía servirse. Finalmente se optó por dos bebidas: cóctel de frutas sin alcohol y zumo de naranjas.Sabemos que…
-20 personas bebieron cóctel de frutas sin alcohol
-10 personas bebieron zumo de naranjas
-8 no concurrieron
-10 personas bebieron zumo de naranjas
-8 no concurrieron
Lo que queremos saber, es ¿cuántas de las personas que concurrieron, se sirvieron de las dos bebidas?
Procedimiento de resolución
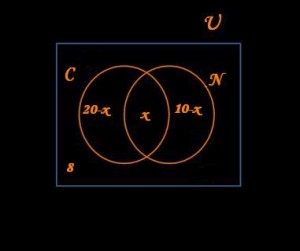
Te conviene disponer en esta ocasión, dos diagramas de Venn contenidos (como siempre) en un rectángulo “universo”. Al primero de los conjuntos le llamaremos C (por cóctel) y al segundo de ellos le llamaremos N (por naranja) y ambos se interceptan, es decir, habrá un espacio donde contener precisamente lo que es la incógnita de este problema, vale decir cuántas personas se sirvieron ambas bebidas. A este número de personas, por ser nuestra incógnita, le llamaremos “x”.
Es importante definir desde el principio cómo le llamaremos a la incógnita, pues habrá que restarla a los datos que nos da el problema, es decir a las 20 personas que sabemos certeramente que bebieron cóctel hay que restarle las que además bebieron zumo.
De este modo y con un razonamiento análogo para los que bebieron zumo (hay que restarle los que además bebieron cóctel), los sectores quedarían definidos de este modo:
- 20 – x = son las personas que bebieron cóctel pero no zumo
- x = son las personas que bebieron cóctel y zumo
- 10 – x = son las personas que bebieron zumo pero no cóctel
Por fuera de los diagramas de Venn, pero formando parte del “universo” hay que ubicar las 8 personas que no asistieron a la celebración.
Queda más claramente expresado, a través del siguiente diagrama de Venn:
Como siempre, el paso siguiente, es expresar todo lo antes razonado a través de una ecuación. En este caso, tenemos claro que la totalidad de personas antes señalada y analizada, suma un total de 30, por lo que esta sería la ecuación que debemos plantear y su correspondiente resolución:
(20 – x) + x + (10 – x) + 8 = 30
20 – x + x + 10 – x + 8 = 30
38 – x = 30
– x = 30 – 38
– x = – 8
x = 8
20 – x + x + 10 – x + 8 = 30
38 – x = 30
– x = 30 – 38
– x = – 8
x = 8
La respuesta final a nuestro problema, es que son 8 las personas que bebieron ambas cosas, vale decir, cóctel de frutas sin alcohol y zumo de naranja.
ejemplo de plantear un problema con conjuntos:
BREVE HISTORIA DE LOS NÚMEROS
NUMERACIÓN DECIMAL
Números naturales
El conjunto de los números naturales se representa por IN y corresponde al siguiente conjunto numérico:
IN = {1, 2, 3, 4, 5, 6, 7, ........}
Los números naturales son un conjunto cerrado para las operaciones de la adición y la multiplicación, ya que al operar con cualquiera de sus elementos, resulta siempre un número perteneciente a IN.
Ejemplo: 2 + 6 = 8, el 8 pertenece a IN.
5 · 3 = 15, el 15 pertenece a IN.
No ocurre lo mismo con las operaciones inversas, o sea, la sustracción y la división. Ellas no son operaciones cerradas en IN.
Ejemplo: 3 - 5 = -2, y -2 no es un elemento de IN.
1 : 4 = 0,25; y 0,25 no es un elemento de IN.
En los números naturales se cumplen las siguientes propiedades para la adición:
Conmutatividad: a + b = b + a, con a y b pertenecientes a IN
Esto se puede apreciar claramente, ya que 3 + 6 = 9, es lo mismo que 6 + 3 = 9.
Asociatividad: (a + b) + c = a + (b + c), con a, b y c pertenecientes a IN
Verifiquemos que (5 + 2) + 6 = 5 + (2 + 6). Resolvamos los paréntesis:
7 + 6 = 5 + 8
13 = 13
En los números naturales se cumplen las siguientes propiedades para la multiplicación:
Conmutatividad: a · b = b · a, con a y b pertenecientes a IN
Esto se puede apreciar claramente, ya que 3 · 6 = 18, es lo mismo que 6 · 3 = 18.
Asociatividad: (a + b) + c = a + (b + c), con a, b y c pertenecientes a IN
Verifiquemos que (5 · 2) · 6 = 5 · (2 · 6). Resolvamos los paréntesis:
10 · 6 = 5 · 12
60 = 60
Elemento Neutro: a · 1 = a, con a perteneciente a IN.
Todo elemento de IN multiplicado por 1, resulta el mismo elemento. 5 · 1 = 5; 9 · 1 = 9 ...
Distributividad: a·(b + c) = a·b + a·c, con a, b y c pertenecientes a IN.
Verifiquemos que 5·(3 + 6) = 5·3 + 5·6
5·9 = 15 + 30
45 = 45
APLICANDO LO APRENDIDO
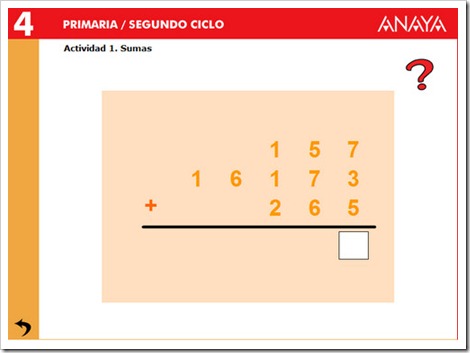
SUMA
La suma es la operación matemética que resulta al reunir en una sola varias cantidades. También se conoce la suma como adición.
a + b = c
Los términos de la suma, a y b, se llaman sumandos y el resultado, c, suma.
Para su notación se emplea entre los sumandos el signo + que se lee "más".
Propiedades de la suma de números naturales
1. Interna:
El resultado de sumar dos números naturales es otro número natural.
a + b 

2. Asociativa:
El modo de agrupar los sumandos no varía el resultado.
(a + b) + c = a + (b + c)
(2 + 3) + 5 = 2 + (3 + 5)
5 + 5 = 2 + 8
10 = 10
3. Conmutativa:
El orden de los sumandos no varía la suma.
a + b = b + a
2 + 5 = 5 + 2
7 = 7
4. Elemento neutro:
El 0 es el elemento neutro de la suma porque todo número sumado con él da el mismo número.
a + 0 = a
3 + 0 = 3
La resta
Los términos de la resta son el minuendo, el sustraendo y la diferencia
1 5
- 7
8
|
Minuendo
Sustraendo
Diferencia
|
La prueba de la resta consiste en comprobar que la suma del sustraendo y la diferencia es igual al minuendo.
15
- 8
7
|
Minuendo
Sustraendo
Diferencia
|
7
+ 8
1 5
|
Sustraendo
Diferencia
Minuendo
|
La multiplicación
La multiplicación es una suma de sumandos iguales.
2 + 2 + 2 = 6 2 x 3 = 6
Los términos de la multiplicación se llaman factores y el resultado se llama producto.
1 2
x 6
7 2
|
Factores
Producto
|
La multiplicación cumple las propiedades conmutativa, asociativa y distributiva.
- Propiedad conmutativa
En una multiplicación se puede cambiar el orden de los factores y se obtiene el mismo producto.
5x4=4x5
|
20=20
|
- Propiedad asociativa
En una multiplicación de varios factores se pueden asociar dos o más factores sin que cambie el resultado.
(5x4) x 2 =5 x (4 x 2)
|
20 x 2=5 x 8
|
40 = 40
|
- Propiedad distributiva
Si se multiplica un número por una suma o una resta se obtiene el mismo resultado que si se multiplica dicho número por cada uno de los términos de la operación y se suman o se restan los productos obtenidos.
2 x (3 + 4) = 2 x 3 + 2 x 4
2 x 7 = 6 + 8
14 = 14
Operaciones combinadas
Para calcular una serie de operaciones combinadas se siguen estos pasos:
· Primero, se calculan las operaciones que hay dentro del paréntesis.
· Luego, se calculan las multiplicaciones.
· Después, se calculan las sumas y las restas en el orden que aparecen.
|
|
Estimaciones
Para estimar el valor de una cantidad se aproxima a las decenas, a las centenas o a los millares, según proceda.
586 + 323 = 590 + 320 = 910 (Se aproxima a las decenas).
586 + 323 = 600 + 300 = 900 (Se aproxima a las centenas).
MULTIPLICACIÓN
Multiplicar dos números naturales consiste en sumar uno de los factores consigo mismo tantas veces como indica el otro factor.
Por ejemplo, la multiplicación 2·5 consiste en sumar el número 2 cinco veces.
a · b = c
Los términos que intervienen en una multiplicación se denominan:
 a y b se denomina factores
a y b se denomina factores El resultado (c) se denomina producto
El resultado (c) se denomina productoPropiedades de la multiplicación de números naturales
1 Operación interna
El resultado de multiplicar dos números naturaleses otro número natural.
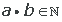
2 Asociativa
El modo de agrupar los factores no varía el resultado.
(a · b) · c = a · (b · c)
3 Conmutativa
El orden de los factores no varía el producto.
a · b = b · a
4 Elemento neutro
El 1 es el elemento neutro de la multiplicación de números naturales porque todo número multiplicado por él da el mismo número.
a · 1 = 1 · a = a
5 Distributiva
La multiplicación de un número natural por una suma es igual a la suma de las multiplicaciones de dicho número natural por cada uno de los sumandos.
a · (b + c) = a · b + a · c
6 Sacar factor común
Es el proceso inverso a la propiedad distributiva.
Si varios sumandos tienen un factor común, podemos transformar la suma en producto extrayendo dicho factor.
a · b + a · c = a · (b + c)
DIVISIÓN
La división de números naturales puede ser:
Exacta: si el resto es igual a cero.Inexacta o entera: si el resto no es cero (aunque siempre tiene que ser menor que el divisor)
Para comprobar si una división está bien resuelta se aplica la “Propiedad fundamental de la división”:
Dividendo = Divisor x Cociente + Resto
Ejemplo:
30 : 7 = 4 (resto 2)Aplicamos la propiedad fundamental de la división:Divisor x Cociente + Resto = 7 x 4 + 2 = 28 + 2 = 30 = DividendoPor lo tanto la división está bien resuelta.
Vemos a continuación como en una división mal resuelta no se cumple esta propiedad:
30 : 7 = 3 (resto 4)Divisor x Cociente + Resto = 7 x 3 + 4 = 21 + 4 = 25 (no = Dividendo)
JUEGO Y APRENDO
¿QUIERES SER MILLONARIO?
CRITERIOS DE DIVISIBILIDAD
Muchas veces no es necesario hacer la división para saber si un número es divisible por otro o no.
Números divisibles por 2
|
Números divisibles por 3
| |
2 12 22 32 ... terminan en 2
4 14 24 34 ... terminan en 4
6 16 26 36 ... terminan en 6
8 18 28 38 ... terminan en 8
10 20 30 40 ... terminan en 0
|
3 12 21 30 ... sus cifras suman 3
6 15 24 33 ... sus cifras suman 6
9 18 21 36 ... sus cifras suman 9
|

|
Para saber si un número es divisible por 10 o por 5, tampoco necesitamos hacer la división.
Números divisibles por 5
|
Números divisibles por 10
| |
10 20 30 40 .... terminan en 0
|
10 40 70 100..
20 50 80 110 .. Todos terminan en 0
30 60 90 ..
|

|
COMPRUEBA SI LO HAS COMPRENDIDO
 Haz clic en las actividades:
Haz clic en las actividades: | Actividad 1 Ahora vamos a conocer los DIVISORES con otra actividad de Mario Ramos.  También nos muestra Mario como podemos calcular los divisores de un número, presta mucha atención ya que haremos algunos ejercicios de este tipo en tu cuaderno. También nos muestra Mario como podemos calcular los divisores de un número, presta mucha atención ya que haremos algunos ejercicios de este tipo en tu cuaderno. Si quieres ver como calculamos los divisores de un número, de forma más gráfica y manipulativa, podemos hacerlo conlas Regletas de Cuisenaire.  Recordamos los criterios para saber si un número es divisible por 2, 3, 5, 9 ó 10. Y hacemos unos ejercicios muy interesantes para memorizar estos criterios y ponerlos en práctica.  |
SEGUIR PRACTICANDO CLICK AQUI































eeeeeeeeeees muuuuuuuuuuuuuuuuuuuuchoooooooooooooooooooooooooooooooooooooooo
ResponderEliminarQue bien profe su pagina es muy buena;);)😎
ResponderEliminar